REFLEXIÓN SOBRE EL BLOG
FUNCIONES
TRIGONOMETRÍA
Definición:La trigonometría es una rama de la matemática, cuyo significado etimológico es 'la medición de los triángulos'

REDUCCIÓN AL PRIMER CUADRANTE
Un ángulo puede estar situado en cualquiera de los cuatro cuadrantes de la circunferencia. Los valores de sus correspondientes razones trigonométricas dependen de su posición.
Cuando un ángulo se encuentra situado en el segundo, tercero o cuarto cuadrante siempre es posible relacionarlo con otro del primer cuadrante cuyas líneas trigonométricas tengan los mismos valores absolutos.
Las relaciones entre las razones trigonométricas de los ángulos situados en los distintos cuadrantes resultaba esencial cuando no se disponía de calculadoras. Existían tablas con los valores de las razones para ángulos del primer cuadrante. Los demás ángulos no figuraban en la tabla pues no era necesario: bastaba con reducirlo al primer cuadrante.
RELACIÓN ENTRE LAS RAZONES TRIGONOMÉTRICAS DE ÁNGULOS SUPLEMENTARIOS
Ángulos suplementarios son los que suman 180º. Si el valor de un ángulo es "A", el valor del suplementario será "180º-A".
La relación de las razones trigonométricas de un ángulo con las de su suplementario va a permitir "reducir" ángulos del segundo al primer cuadrante.
sen (180º-A) = segmento (180º-A)N = segmento AM = sen A
cos(180º-A) = segmento ON = - segmento OM = - cos A
cos(180º-A) = segmento ON = - segmento OM = - cos A
y haciendo el cociente de seno entre coseno:
tg (180º-A) = sen (180º-A)/cos(180º-A) = sen A / - cos A = - tg A
En conclusión, las relaciones existentes entre las razones trigonométricas de ángulos suplementarios son:
sen (180º-A) = + sen A
cos(180º-A) = - cos A
tg (180º-A) = - tg A
cos(180º-A) = - cos A
tg (180º-A) = - tg A
EJEMPLO:
Dado el ángulo 127º reducirlo al primer cuadrante.SOLUCIÓN:El ángulo 127º se encuentra en el segundo cuadrante. Su suplementario es 180º - 127º = 53º, tenemos entonces
sen 127º = sen 53º; cos 127º = - cos 53º; tg 127º = - tg 53º

RELACIÓN ENTRE LAS RAZONES TRIGONOMÉTRICAS DE ÁNGULOS QUE SE DIFERENCIAN EN 180º
La relación de las razones trigonométricas de un ángulo A con las de 180º+A va a permitir "reducir" ángulos del tercer al primer cuadrante.
Como puede observarse en la figura, los triángulos OMA y ON(180º+A) son iguales ya que siendo rectángulos tienen la hipotenusa y un ángulo agudo: ángulo AOM = ángulo (180º-A)ON
Así que:
sen (180º+A) = segmento (180º+A)N = - segmento AM = - sen A
cos(180º+A) = segmento ON = - segmento OM = - cos A
cos(180º+A) = segmento ON = - segmento OM = - cos A
y haciendo el cociente de seno entre coseno
tg (180º+A) = sen (180º+A)/cos(180º+A) = - sen A / - cos A = tg A
sen (180º+A) = - sen A
cos(180º+A) = - cos A
tg (180º+A) = + tg A
cos(180º+A) = - cos A
tg (180º+A) = + tg A
EJEMPLO:
Dado el ángulo 215º reducirlo al primer cuadranteSOLUCIÓN:El ángulo 215º se encuentra en el tercer cuadrante. Este ángulo se diferencia 180º con 215º - 180º = 35º , tenemos entonces
sen 215º = - sen 35º; cos 215º = - cos 35º; tg 215º = tg 35º
RELACIÓN ENTRE LAS RAZONES TRIGONOMÉTRICAS DE ÁNGULOS OPUESTOS
Si el valor de un ángulo es "A", el valor de su opuesto es obviamente -ALa relación de las razones trigonométricas de un ángulo A con las de su opuesto -A va a permitir "reducir" ángulos del cuarto al primer cuadrante.
Los triángulos OMA y ON(-A) son iguales ya que siendo rectángulos tienen igual la hipotenusa (OA = O(-A)) y un ángulo agudo: ángulo AOM = ángulo (-A)ON = A
Por eso:
sen (-A) = segmento (-A)N = - segmento MA = - sen A
cos(-A) = segmento ON = segmento OM = cos A
y haciendo el cociente de seno entre coseno
tg (-A) = sen (-A)/cos(-A) = - sen A / cos A = - tg A
sen (-A) = - sen A
cos(-A) = - cos A
tg (-A) = + tg A
cos(-A) = - cos A
tg (-A) = + tg A
EJEMPLO:
Dado el ángulo 330º reducirlo al primer cuadranteSOLUCIÓN:El ángulo 330º se encuentra en el cuarto cuadrante. Este ángulo viene representado por el mismo radio vector que el ángulo -30º, tenemos entonces
sen 330º = sen (-30º) = - sen 30º ; cos 330º = cos (-30º) = cos 30º; tg 330º = tg ( -30º) = - tg 30º
 Aquí tienen una imagen que les puede ayudar:
Aquí tienen una imagen que les puede ayudar: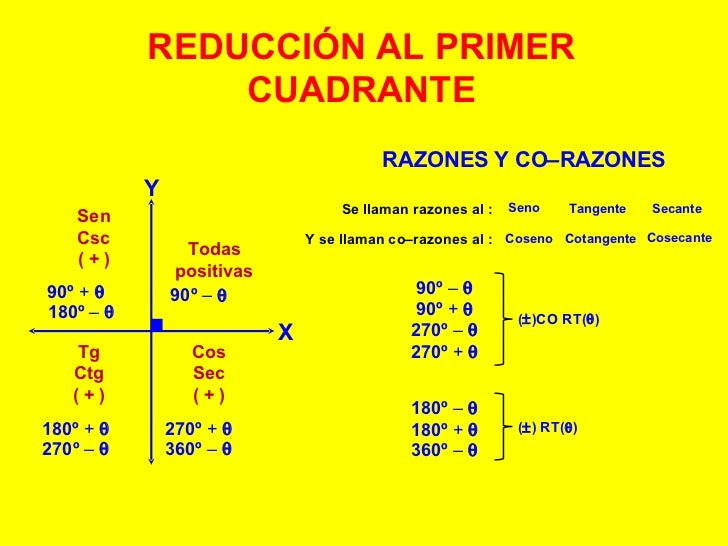
Si no les ha quedado claro les recomiendo que se miren este video:
https://www.youtube.com/watch?v=3Nh-Jynv46E
¿CÓMO PASO DE RADIANES A GRADOS Y DE GRADOS A RADIANES?
GRADOS --> RADIANES
Para pasar de grados a radianes lo hacemos mediante una regla de tres, teniendo en cuenta la equivalencia entre radianes y grados.
Por ejemplo, ¿cuántos radianes son 60º?
Planteamos la regla de tres: Si 180º son π radianes, 60º serán x radianes. Ponemos los grados debajo de los grados y los radianes debajo de los radianes:

Y ahora despejamos la x:

Ya sólo nos queda operar. Para dejarlo el resultado en múltiplos de π , simplificamos los números que tenemos en la operación y nos queda:

Por tanto, 60º equivalen a π /3 radianes:
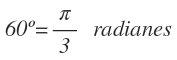
Como te he comentado antes, no es obligatorio dejar los radianes en función de π , por lo que si te es más fácil, puedes sustituir π por 3,14 y operar con la calculadora, cuyo resultado será:
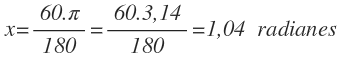
RADIANES --> GRADOS
Para pasar de radianes a grados, lo hacemos igual que antes, con una regla de 3, solo que esta vez, la incógnita a despejar serán los grados.
Ejemplo:
¿Cuántos grados son 3π /4 radianes?
Planteamos la regla de tres: Si π radianes son 180º, 3π/4 radianes seran x grados:

Despejamos la x y resolvemos:
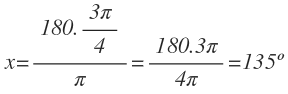
Por tanto 3π/4 radianes equivalen a 135º
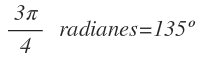
Grados y radianes en las razones trigonométricas con la calculadora
Para calcular las razones trigonométricas tanto en grados como en radianes es necesario que la calculadora la pongas en modo “grados” o en modo “radianes”.
Por defecto, la calculadora está en “grados” y para trabajar con radianes hay que cambiarla a “radianes”, pero mucho cuidaddo, porque es muy habitual cambiarla a “radianes” y olvidarse y luego trabajar con grados, entonce estará todo mal.
Asegúrate que la calculadora está siempre en el modo que quieres.
Si calculas el seno de 90º con la calculadora (que por defecto está en “grados”), verás que el resultado es 1:

Si pasas 90º a radianes, verás que 90º=π/2 radianes, por lo que el seno de π/2 también es 1:
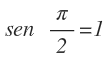
Sin embargo, si calculas el seno de π/2 con la calculadora en “grados”, el resultado no será el correcto, ya que te dará 0,027:

Ya que realmente estarás calculando el seno de 1,57º (que es el resultado de dividir π entre 2).
Para calcular el seno de π/2 correctamente y que el resultado sea 1, entonces la calculadora debe estar en “radianes”.
Es un despiste muy frecuente, así que asegurate siempre de que la tienes en el modo correcto.
Y como siempre, aquí tienen un vídeo:
https://www.youtube.com/watch?v=S5xmJTmqQFA

Las identidades trigonométricas son ecuaciones que contienen funciones trigonométricas.
Es decir, la comparación por su cociente de sus tres lados a, b y c.
Éstas son:
Cosecante del ángulo complementario:
Tangente del ángulo suplementario:
Cotangente del ángulo suplementario:
Coseno del ángulo que difiere 180º
Cotangente del ángulo que difiere 180º:










Descubierto el número primo más largo, con 23 millones de cifras
Un ingeniero estadounidense de 51 años supera el anterior récord por casi un millón de dígitos.

RAZONES TRIGONOMÉTRICAS
Las identidades trigonométricas son ecuaciones que contienen funciones trigonométricas.

Las razones trigonométricas de un ángulo α son las razones obtenidas entre los tres lados de un triángulo rectángulo.
Es decir, la comparación por su cociente de sus tres lados a, b y c.
Sea α uno de los ángulos agudos del triángulo rectángulo.
El seno de un ángulo α se define como la razón entre el cateto opuesto (a) y la hipotenusa(c).

El coseno se define como la razón entre el cateto contiguo o cateto adyacente (b) y la hipotenusa (c).

La tangente es la razón entre el cateto opuesto (a) y el cateto contiguo o cateto adyacente (b).


Razones trigonométricas recíprocas
Las razones trigonométricas recíprocas (o recíprocas) son los inversos multiplicativos de las razones trigonométricas.
Éstas son:
Cosecante (csc): es la razón inversa del seno. Es decir, csc α · sen α=1.
Secante (sec): la razón inversa del coseno. Es decir, sec α · cos α=1
Cotangente (cot): es la razón inversa de la tangente. También en este caso, cot α · tan α=1
Relación entre razones trigonométricas

Nota: el signo ± que corresponde en cada caso depende del cuadrante en que esté el ángulo.
Relaciones trigonométricas básicas
Identidad fundamental de la trigonometría

Relación entre el seno, coseno y tangente

Relación trigonométrica entre la tangente y la secante

Relación trigonométrica entre la cosecante y la cotangente

Ángulos complementarios
Seno del ángulo complementario:

Coseno del ángulo complementario:

Tangente del ángulo complementario:

Cosecante del ángulo complementario:

Secante del ángulo complementario:

Cotangente del ángulo complementario:

Ángulos suplementarios
Seno del ángulo suplementario:

Coseno del ángulo suplementario:

Tangente del ángulo suplementario:

Cosecante del ángulo suplementario:

Secante del ángulo suplementario:

Cotangente del ángulo suplementario:

Ángulos conjugados
Seno del ángulo conjugado:

Coseno del ángulo conjugado:

Tangente del ángulo conjugado:

Cosecante del ángulo conjugado:

Secante del ángulo conjugado:

Cotangente del ángulo conjugado:

Ángulos opuestos
Seno del ángulo opuesto:

Coseno del ángulo opuesto:

Tangente del ángulo opuesto:

Cosecante del ángulo opuesto:

Secante del ángulo opuesto:

Cotangente del ángulo opuesto:

Ángulos que difieren 90º
Seno del ángulo que difiere 90º

Coseno del ángulo que difiere 90º:

Tangente del ángulo que difiere 90º:

Cosecante del ángulo que difiere 90º:

Secante del ángulo que difiere 90º:

Cotangente del ángulo que difiere 90º:

Ángulos que difieren 180º
Seno del ángulo que difiere 180º:

Coseno del ángulo que difiere 180º

Tangente del ángulo que difiere 180º:

Cosecante del ángulo que difiere 180º:

Secante del ángulo que difiere 180º:

Cotangente del ángulo que difiere 180º:

Y como no, nuestro vídeo:
https://www.youtube.com/watch?v=He7SY4kFDVA
TEOREMA DEL SENO Y DEL COSENO
Teorema del seno
Ejemplo
Resolver un triángulo con los siguientes datos: a = 4 cm, b = 5 cm y B = 30º
- Dibujamos el triángulo, nombramos los ángulos y lados, colocamos los datos conocidos y resolvemos. Resolver un triángulo es decir lo que valen sus 3 ángulos y sus 3 lados.
Teorema del coseno
Ejemplo
Resolver un triángulo con los datos siguientes: a = 1200 m, c= 700 m y B = 108º
- Dibujamos el triángulo, nos dan 2 lados y el ángulo que forman.
Calculamos el lado b aplicando el teorema del coseno.
ECUACIONES TRIGONOMÉTRICAS USANDO LAS IDENTIDADES TRIGONOMÉTRICAS
Una ecuación que contiene funciones trigonométricas es llamada una ecuación trigonométrica
Ejemplo:

Las identidades trigonométricas son ecuaciones que involucran las funciones trigonométricas que son verdaderas para cada valor de las variables involucradas. Puede usar las identidades trigonométricas junto con los métodos algebraicos para resolver las ecuaciones trigonométricas.
Ejemplo :

La ecuación contiene tanto la función seno como coseno.
Reescribimos la ecuación para que solo contenga funciones coseno sin 2 x = 1 – cos 2 x .

Factorizando cos x obtenemos, cos x (2 cos x + 1) = 0.
Usando la propiedad del producto cero , obtendremos cos x = 0, y 2cos x + 1 = 0 lo que nos arroja cos x = –1/2.
En el intervalo [0, 2 π ), sabemos que cos x = 0 cuando x = π /2 y x = 3 π /2. Por otro lado, también sabemos que cos x = –1/2 cuando x = 2 π /3 y x = 4 π /3.
Por lo tanto, las soluciones de la ecuación dada son

PREGUNTAS PERSONALES SOBRE TRIGONOMETRÍA:
¿Qué es lo más importante que he aprendido de esta unidad y durante el tiempo en el que transcurrió?
Pienso que la trigonometría en sí ya es importante, no hay nada que "resalte" por decirlo de alguna manera.
¿Qué dificultades, preguntas o dudas se me plantean?
Sinceramente, pienso que este tema es uno de los más difíciles junto al Álgebra, así que sigo teniendo dudas con las ecuaciones por ejemplo.
¿Qué consecuencias tiene tiene lo aprendido con mi vida, a nivel personal y académico?
Académicamente, me sirve para resolver problemas y aprobar exámenes aunque no me sirve mucho para la vida real, tal vez para alguien que quiera una carrera de ingeniería o de un grado en matemáticas.
¿Para qué sirve?¿Qué puedo hacer yo con ello?
Sirve para la resolución de triángulos y todo lo que tenga que ver con ellos.
NOTICIA MATEMÁTICA
Descubierto el número primo más largo, con 23 millones de cifras
Un ingeniero estadounidense de 51 años supera el anterior récord por casi un millón de dígitos.
Un ingeniero eléctrico estadounidense de 51 años, Jonathan Pace, ha descubierto el número primo más largo conocido hasta la fecha, con más de 23 millones de cifras, según ha anunciado su equipo en un comunicado
. Los números primos son aquellos que solo se pueden dividir por sí mismos y por la unidad, como 2, 3, 5, 7, 11, 13, 17… Están considerados los átomos de las matemáticas, sus ladrillos indivisibles, ya que cualquier número entero se puede descomponer como el producto de unos primos. Por ejemplo, 12 es 3 x 2 x 2, descompuesto en primos.
El número hallado por Pace pertenece a una familia especial de números primos, la de los primos de Mersenne. Responden a la forma 2n – 1. Por ejemplo, 22 – 1 = 3, así que 3 es el primer primo de Mersenne. En el año 1588, el matemático italiano Pietro Cataldi demostró que 217 – 1 = 131.071, el mayor primo de Mersenne hasta entonces. En todos estos siglos, la humanidad solo había encontrado 49 primos de esta familia. El detectado ahora por Pace es el quincuagésimo. Se obtiene con la fórmula 277.232.917 – 1 y tiene 23.249.425 cifras, casi un millón más que el anterior record, obtenido hace dos años.
La búsqueda de estos primos gigantescos no es un mero pasatiempo, según explica Manuel de León, director del Instituto de Ciencias Matemáticas (ICMAT), en Madrid. El algoritmo criptográfico RSA, que se utiliza para garantizar la seguridad del intercambio de información en la web, está basado en esta descomposición de números enteros en números primos. Cuanto más grandes sean estos, más difícil será romper el código. Las transacciones comerciales por internet y la privacidad de las comunicaciones dependen en parte de los números primos.
Jonathan Pace vive en Germantown, una pequeña ciudad a las afueras de Memphis, y trabaja para la empresa de logística FedEx. Es uno de los miles de voluntarios de GIMPS, un proyecto colaborativo para buscar números primos de Mersenne por internet, mediante un programa gratuito elaborado por los científicos de la computación George Woltman, Scott Kurowski y Aaron Blosser. Pace mantuvo un ordenador personal con un procesador Intel i5-6600 trabajando durante seis días sin parar hasta demostrar que 277.232.917 – 1 es un número primo. Se llevará una recompensa de 3.000 dólares. La Fundación Fronteras Electrónicas, con sede en San Francisco (EE UU),ofrece 150.000 dólares a la primera persona que encuentre un número primo de 100 millones de cifras.

TRABAJO CON TRIÁNGULOS
Aquí tienen algunos de los triángulos que he hecho en Geogebra:
- Triángulo conocidos sus tres lados
- Triángulo conocidos sus dos lados
- Triángulo conocidos un lado y sus ángulos adyacentes
ÁLGEBRA
Antes que nada, debemos saber que el método de Gauss-Seidel es un método utilizado para resolver sistemas de ecuaciones lineales con 3 incógnitas. Se llama así en honor a los matemáticos Carl Friedrich Gauss y Philipp Ludwig von Seidel y es similar al método de Jacobi.
Para resolver por este método, tenemos que seguir estos 4 sencillos pasos:
El número hallado por Pace pertenece a una familia especial de números primos, la de los primos de Mersenne. Responden a la forma 2n – 1. Por ejemplo, 22 – 1 = 3, así que 3 es el primer primo de Mersenne. En el año 1588, el matemático italiano Pietro Cataldi demostró que 217 – 1 = 131.071, el mayor primo de Mersenne hasta entonces. En todos estos siglos, la humanidad solo había encontrado 49 primos de esta familia. El detectado ahora por Pace es el quincuagésimo. Se obtiene con la fórmula 277.232.917 – 1 y tiene 23.249.425 cifras, casi un millón más que el anterior record, obtenido hace dos años.
La búsqueda de estos primos gigantescos no es un mero pasatiempo, según explica Manuel de León, director del Instituto de Ciencias Matemáticas (ICMAT), en Madrid. El algoritmo criptográfico RSA, que se utiliza para garantizar la seguridad del intercambio de información en la web, está basado en esta descomposición de números enteros en números primos. Cuanto más grandes sean estos, más difícil será romper el código. Las transacciones comerciales por internet y la privacidad de las comunicaciones dependen en parte de los números primos.
Jonathan Pace vive en Germantown, una pequeña ciudad a las afueras de Memphis, y trabaja para la empresa de logística FedEx. Es uno de los miles de voluntarios de GIMPS, un proyecto colaborativo para buscar números primos de Mersenne por internet, mediante un programa gratuito elaborado por los científicos de la computación George Woltman, Scott Kurowski y Aaron Blosser. Pace mantuvo un ordenador personal con un procesador Intel i5-6600 trabajando durante seis días sin parar hasta demostrar que 277.232.917 – 1 es un número primo. Se llevará una recompensa de 3.000 dólares. La Fundación Fronteras Electrónicas, con sede en San Francisco (EE UU),ofrece 150.000 dólares a la primera persona que encuentre un número primo de 100 millones de cifras.

TRABAJO CON TRIÁNGULOS
Aquí tienen algunos de los triángulos que he hecho en Geogebra:
- Triángulo conocidos sus tres lados
- Triángulo conocidos sus dos lados
- Triángulo conocidos un lado y sus ángulos adyacentes
ÁLGEBRA
Método de Gauss:
Antes que nada, debemos saber que el método de Gauss-Seidel es un método utilizado para resolver sistemas de ecuaciones lineales con 3 incógnitas. Se llama así en honor a los matemáticos Carl Friedrich Gauss y Philipp Ludwig von Seidel y es similar al método de Jacobi.
Para resolver por este método, tenemos que seguir estos 4 sencillos pasos:
1º Primero, hacemos que la X valga cero utilizando de la segunda ecuación (F2) reduciéndola con la primera ecuación (F1).
( A la segunda y tercera ecuacion se le puede multiplicar números)
2º Después, tenemos que hacer que valga cero la X de la tercera ecuación (F3) reduciéndola con la primera ecuación(F1).
3º Lo siguiente es conseguir que valga cero la Y o la Z de la tercera ecuación (F3) jugando con la segunda (F2) y la tercera ecuación (F2).
4º Y por último,con este sistema podemos obtener las soluciones haciendo las ecuaciones de primer grado.
Imagen de : http://profe-alexz.blogspot.com.es/2012/08/metodo-gauss-sistema-ecuaciones-4x4.html
Este vídeo les ayudará:
https://www.youtube.com/watch?v=-PWtVxzmhOo
INECUACIONES:
INECUACIONES
Es una DESIGUALDAD entre dos expresiones algebraicas de una o varias incógnitas, que solo se verifica para ciertos valores de esas incógnitas; se expresa con los signos >, <, ≥ y ≤.
"< " Menor que "≤." Menor o igual que
Se puede representar en dos distintas formas:
1º La recta real
2º En intervalo/s
Las inecuaciones trata de poner todos los valores de "x" juntos y todos los demás al otro lado
PRIMER GRADO:
SEGUNDO GRADO
Les dejo un vídeo por aquí para que lo pilléis mejor con mi profesor youtuber favorito:
SISTEMAS DE INECUACIONES
Primer Grado:
Cuando tenemos un sistema de desigualdades resolvemos cada una de ellas por separado, la solución va a ser la común a las desigualdades.
Segundo Grado
Para resolver desigualdades de segundo grado o de grado superior es necesario descomponer en factores. Recuerda que para hacer la descomposición factorial dependiendo de la ecuación podemos sacar factor común, resolver la ecuación de segundo grado o aplicar la regla de Ruffini.
FRACCIONES ALGEBRÁICAS:
Una fracción algebraica es una expresión fraccionaria en la que numerador y denominador son polinomios, siendo el denominador no nulo. Son fracciones algebraicas: Las fracciones algebraicas tienen un comportamiento similar a las fracciones numéricas a la hora de trabajar con ellas.
Hay que saber que:
- Numerador: la parte de arriba de la fracción (por ejemplo (x+5)/(2x+3)).
- Denominador: la parte inferior de la fracción (por ejemplo (x+5)/(2x+3)).
- Común denominador: este es el número que puedes dividir entre los números de la parte superior y la inferior. Por ejemplo, en la fracción 3/9, el común denominador es 3, ya que ambos números son divisibles entre 3.
- Factor: un número que se multiplica para tener otro. Por ejemplo, los factores de 15 son 1, 3, 5 y 15. Los factores de 4 son 1, 2 y 4.
- Ecuación simplificada: consiste en eliminar todos los factores comunes y agrupar variables similares (5x + x = 6x) hasta tener la forma más básica de una fracción, ecuación o problema. Si no puedes hacer nada más con la fracción, ya está simplificada.
Después, resolvemos fracciones simple. .
35 → 5 * 7
Ya puedes cancelar los términos semejantes. En este caso, puedes cancelar los dos cincos, dejando la respuesta simplificada de 3/7.
¿QUÉ TE HA PARECIDO EL EXAMEN POR PAREJAS?
Me ha parecido dentro de lo que cabe un poco difícil pero se puede justificar con que era en parejas, aunque aparte de la dificultad, ha estado bien y claro.
¿HAS APRENDIDO ALGO NUEVO MIENTRAS LO HACÍAS?¿QUÉ?HE RECORDADO A DIVIDIR EN FRACCIONES Y EN LA CORRECCIÓN HE APRENDIDO A TENER MUCHO CUIDADO CON LOS SIGNOS, PORQUE PUEDE CAMBIARLO TODO.
¿QUÉ TE HA PARECIDO TRABAJAR CON LA PAREJA ELEGIDA?
Pues bien, ya que en algunos casos nos dábamos cuenta de los fallos que cometíamos uno y el otro.
¿ESTABAN AJUSTADAS LAS PREGUNTAS A LO QUE HABÍAMOS TRABAJADO EN CLASE?
Todo el temario lo hemos visto, aunque en el examen hubo más dificultad que en cualquier ejercicio realizado en clase.
¿LES DIO TIEMPO? ¿QUÉ QUITARÍAS O PONDRÍAS?
No nos dio tiempo y lo que haría sería reemplazar algún ejercicio que se necesite más tiempo por otro menos complejo.
😬NUEVO CURSO 😬
¡Hola a todos! Bueno, acabo de empezar un nuevo curso, 1º de Bachillerato de Ciencias y sí, eso significa más contenido nuevo en Mates! Todavía estamos a principios de Noviembre pero, hemos dado temas que les podría interesar,aparte, daré mi reflexión sobre cada tema ¡Empecemos!📚
NÚMEROS REALES😵
Números reales desde mi opinión es un tema muy sencillo ya que se basa en la clasificación de números desde números positivos, (que hemos visto desde primaria) hasta irracionales y radicales.
Se repite cada año y hacen muy bien, es un tema básico y significativo en el mundo matemático.
Me ha sido fácil aprenderme el tema y opino que es uno de lo más importantes de las matemáticas.
Algunas preguntas que se me han pasado por la cabeza aprendiendo los números reales son ínfimas, ahora todo lo que sé de números reales:
¿Qué es un número real?😕
La definición más clara sería que son todos los número que encontramos en la recta real. Esto incluye a los negativos,positivos, fracciones, irracionales, etc.
La definición más clara sería que son todos los número que encontramos en la recta real. Esto incluye a los negativos,positivos, fracciones, irracionales, etc.
Recuerden que entre el 1 y el 2 (por ejemplo) hay infinitos números al igual que con todos los números en la recta.
Con estas circunferencias quiero enseñar que TODOS los números son reales aunque estén en diferentes grupos
REPRESENTACIÓN DE NÚMEROS REALES EN LA RECTA REAL 🙋
En la recta, la representación de números reales se puede hacer con una exactitud aproximada, sin embargo, se pueden usar técnicas para representarlos de forma exacta. Como en el siguiente ejemplo de :
Allí se puede ver que la raíz de 7 se puede descomponer
Primero se descompone 7 en suma de cuadrados:
Primero se descompone 7 en suma de cuadrados:
💙Los sumandos serán los puntos en el eje cartesiano que nos darán la ubicación del número en cada uno de los ejes del plano. La raíz de tres. Para ello primero representaré
 Se obtiene al trazar un triángulo cuyos catetos tengan valor de uno y cuya hipotenusa será igual a . El vértice superior luego se debe trasladar de forma circular y con pivote en cero hasta llegar a la línea horizontal o eje X:
Se obtiene al trazar un triángulo cuyos catetos tengan valor de uno y cuya hipotenusa será igual a . El vértice superior luego se debe trasladar de forma circular y con pivote en cero hasta llegar a la línea horizontal o eje X:Ahora descomponemos , obtenemos que:

💙Por lo tanto, en la recta se debe ubicar un punto entre estos dos números, sean
y de tal modo que el gráfico, sobre el gráfico anterior quedaría de esta manera:
Cuando ya tenemos la ubicación de en el eje X y de en el eje Y. Ahora se procede a ubicar a en la recta real, así:

NOTACIÓN CIENTÍFICA
( Recordatorio de la notación científica está también a principio de la página)
La notación científica es un tema ya dado en 4º de Secundaria pero daré mi conclusión igualmente.
Este tema es mi FAVORITO y aún no sé porqué . He pensado que puede ser por la facilidad del tema, pero tengo en cuenta que hay temas aún más fáciles.
Puede ser porque la notación científica no la aprendí en clase, si no con mi padre y de ahí también con la ayuda de internet.
Sirve para CUALQUIER cosa, y, para lo más fundamental, el Cáculo Mental.
No me costó en absoluto este tema, fue uno de los más fáciles de toda mi vida en matemáticas.
DEFINICIÓN: La notación científica es un recurso matemático que sirve para simplificar cálculos y representar en forma breve números muy grandes o muy pequeños. Para hacerlo se usan las potencias de 10.
EL NÚMERO MULTIPLICADO POR LA POTENCIA DE 10 (N) SERÁ ENTRE 1 Y 10.
Su fórmula es: N X 10^x
Para expresar el número en notación científica:
- Primero: Se identifica la coma decimal (si la hay)
- Segundo:La desplazamos hacia la izquierda (si el exponente de 10 es positivo) o
hacia la derecha (si el exponente de 10 es negativo)
- Tercero: Se rueda la coma tantos lugares como el número de exponente tenga 10 (x)
EJEMPLO:
7,341 X 10^6 = 0,000007341 ( Se a rotado la coma 6 veces)
2,3654 X 10^-4 = 23654 ( Se ha rotado la coma 4 veces)
¿CÓMO MULTIPLICAR CON NOTACIÓN CIENTÍFICA?
Primero tenemos que saber las dos notaciones:
N1 X 10^x1 y N2 X 10^x2
Después, saber cómo multiplicarlas:
N1 X N2 X 10^x1 + x2 (Se suma los dos exponentes de 10 de cada operación)
EJEMPLO:
5,24 X 10^6 Y 6,3 X 10^8
(5,24 X 10^6) X (6,3 X 10 ^8) = 5,24 X 6,3 X 10^6+8 = 33,012 X 10^14 = 3,3012^15
¿CÓMO DIVIDIR CON LA NOTACIÓN CIENTÍFICA?
Primero tenemos que saber las dos notaciones:
N1 X 10^x1 y N2 X 10^x2
Después, saber cómo dividirlas:
(N1: N2) X 10^x1 - x2 ( Se resta los dos exponentes de 10 de cada operación)
EJEMPLO:
5,24 X 10^7 Y 6,3 X 10^4
(5,24 : 6,3)X 10^7-4 = 0,831746 • 10^3= 8,31746 • 10^-1 • 10^3 = 8,31746 • 10^2
Aquí un vídeo que les puede servir de mucho: https://www.youtube.com/watch?v=ok-IRe6ACaI
APROXIMACIÓN,REDONDEO Y TRUCAMIENTO
Sinceramente, este tema es bastante útil, para cualquier cosa, como por ejemplo la contabilidad. Aconsejo que se lo aprendan bien porque se pueden confundir de términos que fue lo que me pasó a mí. Desde mi experiencia con el tema,es muy básico en el ámbito matemático.
No hubo preguntas que no haya sabido la respuesta, o una pregunta muy difícil para destacarla es un tema facilísimo como dije antes y solo hay que cogerle el tranquillo.
¡ÁNIMO!
(La aproximación es una representación inexacta de un número se puede hacer de varios modos:)
Defecto: Buscamos el número con un determinado número de cifras que es inmediatemente menor que el dado.
Defecto: Buscamos el número con un determinado número de cifras que es inmediatemente menor que el dado.
Exceso: Es el número con las cifras decimales fijadas inmediatemente mayor.
Por ejemplo, dado el número 1.3456 vamos a aproximarlo con dos cifras decimales:
- Por defecto es 1.34
- Por exceso es 1.35
Al dar la aproximación en lugar del número se comete un error (la comparación entre el número sin aproximar y el número aproximado), en el ejemplo anterior los errores que se cometen son:
En defecto: | 1.3456 - 1.34 | = 0.0056
En exceso: | 1.3456 - 1.35 | = 0.0044
(Redondear un número consiste en dar la mejor de las aproximaciones, es decir, aquella con la que se comente un error menor)

Por ejemplo:
Si redondeamos 1.3456 a dos cifras decimales, el redondeo será 1.35
Por ejemplo, dado el número 1.3456 vamos a aproximarlo con dos cifras decimales:
- Por defecto es 1.34
- Por exceso es 1.35
Al dar la aproximación en lugar del número se comete un error (la comparación entre el número sin aproximar y el número aproximado), en el ejemplo anterior los errores que se cometen son:
En defecto: | 1.3456 - 1.34 | = 0.0056
En exceso: | 1.3456 - 1.35 | = 0.0044
(Redondear un número consiste en dar la mejor de las aproximaciones, es decir, aquella con la que se comente un error menor)

Por ejemplo:
Si redondeamos 1.3456 a dos cifras decimales, el redondeo será 1.35
(El truncamiento de un número decimal se eliminan las cifras a partir de aquellas en la que se realiza el truncamiento)
Truncamiento por la unidad: Se eliminan todas las cifras decimales.
45,325 se trunca por 45
122,3434 se trunca por 122
91,435123 se trunca por 91
Truncamiento por la décima: tan sólo se deja esta cifra decimal:
45,325 se trunca por 45,3
122,3434 se trunca por 122,3
91,435123 se trunca por 91,4
Truncamiento por la centésima: tan sólo se dejan dos cifras decimales:
45,325 se trunca por 45,32
122,3434 se trunca por 122,34
91,435123 se trunca por 91,43

RADICALES 💜
Radicales podría considerarse uno de los más difíciles de la matemática, me costó muchísimo (a día de hoy me sigue costando) aprendérmelo ya que es complejo, pero todo se basa en practicar. No se asusten porque hayan muchas raíces juntas o divisiones de raíces con índice (fue lo que me pasó) y léanselo bien y despacio. Después de entenderlo, les va a encantar.
Radicales sirve no solo para matemáticas y para clase (en mi opinión) creo que podría servir para muchos programas y al llegar a este tema piensen... por fin esas pizarras infinitas que veíamos en las películas como raíces en raíces o índices inmensos... ¡Ya nosotros sabremos hacerlo y que significa!
Cuando no puedes simplificar un número para quitar una raíz cuadrada (o una raíz cúbica, etc.) entonces es un radical.
Ejemplo: √2 (la raíz cuadrada de 2) no se puede simplificar más así que es un radical.
Pero √4 (la raíz cuadrada de 4) sí se puede simplificar (queda 2), así que no es un radical.
Radicales sirve no solo para matemáticas y para clase (en mi opinión) creo que podría servir para muchos programas y al llegar a este tema piensen... por fin esas pizarras infinitas que veíamos en las películas como raíces en raíces o índices inmensos... ¡Ya nosotros sabremos hacerlo y que significa!
Cuando no puedes simplificar un número para quitar una raíz cuadrada (o una raíz cúbica, etc.) entonces es un radical.
Ejemplo: √2 (la raíz cuadrada de 2) no se puede simplificar más así que es un radical.
Pero √4 (la raíz cuadrada de 4) sí se puede simplificar (queda 2), así que no es un radical.
He encontrado una tabla con ejemplos de números radicales y otros que no, nos ayudará para reconocer los radicales :
| Número | Simplificado | En decimal | ¿Radical o no? |
|---|---|---|---|
| √2 | √2 | 1.4142135(etc) | Radical |
| √3 | √3 | 1.7320508(etc) | Radical |
| √4 | 2 | 2 | No es radical |
| √(1/4) | 1/2 | 0.5 | No es radical |
| 3√(11) | 3√(11) | 2.2239800(etc) | Radical |
| 3√(27) | 3 | 3 | No es radical |
| 5√(3) | 5√(3) | 1.2457309(etc) | Radical |
Si es una raíz e irracional, es un radical.
NOTITA: No todas las raíces son radicales.
ESTRUCTURA Y SOLUCIONES DE LAS RADICALES
OPERACIONES CON RADICALES
SUMA DE RADICALES
Para sumar radicales deben ser semejantes, tener el mismo índice y el mismo radicando
Se suma los coeficientes y se deja el mismo índice y radicando.
Cuando los radicales no son semejantes, para conseguir que lo sean hay que extraer factores fuera del radical.
Ejemplo: √18 + √50 +√2 -√8
1º Descomponemos en factores
√18 + √50 +√2 -√8 = √(2 3^2) + √(2 5^2)+ √2 - √(2^3)
2º Extraemos factores
Para poder extraer factores de un radical, deben tener el mismo exponente que el índice que la raíz y estar multiplicando o dividiendo dentro del radicando.
Si están sumando no se pueden extraer
- En ese caso ya tenemos preparado el 3^2 y el 5^2 para poderlos extraer
√(2 3^2) + √(2 5^2) + √2 - √(2^3) = 3 √2 + 5√2 +√2- √(2^3)
- √( 2^3) lo extraemos y es = 2√2
3º Ya son semejantes, sumamos los coeficientes y dejamos el mismo índice y el mismo radicando
3√2 + 5√2 + √2 - 2√2 7√2
RAÍZ DE LA RAÍZ
( Puede sonar complicado, pero verán que cuando lo veamos poco a poco, se entenderá mejor👍 )☝Cuando hay algún número entre las raíces:
Se multiplican los índices y se deja el mismo radicando
Ejemplo:
👆 Cuando hay algún número entre las raíces:
 Hay que introducir factores en el radical
Hay que introducir factores en el radicalPara introducir factores en un radical:
- Se introduce el factor que sea elevado al mismo índice que tenga la raíz donde lo queramos introducir.
Queremos introducir el 2 que está entre los dos radicales.
El índice de la raíz es 4, así que el 2 lo debemos introducir elevado a la cuarta
Después se multiplican los índices y se opera con el radicando.
MULTIPLICACIÓN DE RADICALES
Para multiplicar radicales deben tener el mismo índice
Para multiplicar radicales deben tener el mismo índice
Se deja el mismo índice y se multiplica SOLO los radicandos.



Cuando no tienen el mismo índice primero hay que reducir a índice común
Se hace hallando el mínimo común múltiplo de los índices




DIVISIÓN DE RADICALES
Para dividir radicales deben tener el mismo índice
Para dividir radicales deben tener el mismo índice
Se deja e mismo índice y SOLO se dividen los radicandos.

LOGARITMOS
(no, no es tan difícil como parece)
Logaritmos al ser tan fácil ( desde mi opinión) me da rabia que todavía no tenga un ejemplo de logaritmos en la vida afuera de la clase de matemáticas, pero aún así, sigue siendo la esencia de las matemáticas, no todos saben contestar a la pregunta ¿Qué es un logaritmo?
No se me han ocurrido muchas preguntas o dudas acerca de los logaritmos, ya que lo único que se me puede ocurrir que se puede hacer mal es confundir dónde se pone un "log" en una ecuación o cuando se debería quitar.
Si se le saca provecho al tema, se podría hacer muchos proyectos con solo logaritmos y por ahora osolo tengo una frase para ellos aunque por ahora no me sirvan para nada en concreto... ¡El conocimiento es un don!
Logaritmos al ser tan fácil ( desde mi opinión) me da rabia que todavía no tenga un ejemplo de logaritmos en la vida afuera de la clase de matemáticas, pero aún así, sigue siendo la esencia de las matemáticas, no todos saben contestar a la pregunta ¿Qué es un logaritmo?
No se me han ocurrido muchas preguntas o dudas acerca de los logaritmos, ya que lo único que se me puede ocurrir que se puede hacer mal es confundir dónde se pone un "log" en una ecuación o cuando se debería quitar.
Si se le saca provecho al tema, se podría hacer muchos proyectos con solo logaritmos y por ahora osolo tengo una frase para ellos aunque por ahora no me sirvan para nada en concreto... ¡El conocimiento es un don!
El logaritmo de un número real positivo (en una base de logaritmo determinada) es el exponente al cual hay que elevar la base para obtener dicho número.
Por ejemplo, el logaritmo en base 10 de 1000 es 3, porque 1000 es igual a 10 a la potencia 3:
1000 = 103 = 10×10×10.
Todos los problemas con logaritmos se resuelven con las siguientes propiedades:
Les pondré un ejercicio resuelto a ver si es más fácil entenderlos así:
Supongamos que: log(base 4)64 = x
Esto significa que 4(elevado a x) = 64
Como 4( elevado a 3) da 64
x=3
Aquí les dejo un video de unicoos, por si no lo entendeis del todo.
4º ESO
POLINOMIOS
Es una expresión hecha con constantes, variables y exponentes, que están combinados usando sumas, restas y multiplicaciones, … pero no divisiones.
Los exponentes sólo pueden ser 0,1,2,3,... etc.

OPERACIONES CON POLINOMIOS
- SUMA: Para sumar dos polinomios,se simplifican los monomios semejantes de ambos polinomios.

- RESTA: Para restar dos polinomios,se suma al mininuendo el opuesto del sustraendo

- DIVISIÓN:
(2 métodos)
Ruffini:
Es la división de un polinomio por un polinomio.
❤ Se divide el primer término del dividendo entre el primer término del
divisor, obteniéndose así el primer término del cociente.
❤ Se
multiplica el primer término del cociente por todo el divisor y el
producto así obtenido se resta del dividendo, para lo cual se le cambia
de signo y se escribe cada término de su semejante. En el caso de que
algún término de este producto no tenga ningún término semejante en el
dividendo, es escribe dicho término en el lugar que le corresponda de
acuerdo con la ordenación del dividendo y del divisor.

GRADO DE UN POLINOMIO
El grado de un polinomio de varias variables es el grado mayor de los términos del polinomio.
 Grado 3.
Grado 3.
VALOR NUMÉRICO DE UN POLINOMIO
El valor numérico de un polinomio, P(x), para un valor x = a, es el número obtenido al sustituir la letra x por el número a y efectuar las operaciones indicadas. A ese número se le llama P(a).
Si P(a) = 0, se dice que a es una raíz o cero del polinomio P(x). Una raíz es una solución de la ecuación P(x) = 0.

INECUACIONES
Es una DESIGUALDAD entre dos expresiones algebraicas de una o varias incógnitas, que solo se verifica para ciertos valores de esas incógnitas; se expresa con los signos >, <, ≥ y ≤.
Las inecuaciones trata de poner todos los valores de "x" juntos y todos los demás al otro lado
PRIMER GRADO:
PARÁBOLAS
Para esta parábola he utilizado GEOGEBRA
Primero, he descargado una foto de Benito Pérez Galdós.
Después he hecho 3 variables, punto "f", "g" y "h".
y otra de mi paseo por Roma (coliseo romano)
Para conseguir estas parábolas he tenido que poner (X - Y)^2
Para que la parábola tenga su punto más alto, he tenido que poner después de (X-Y)^2 - Z
Para que la parábola tenga su punto más bajo, he tenido que poner después de (X´-Y)^2 +Z
PARÁBOLAS INVERSAS
BICUADRADAS
IMPORTANTE
❤ Se
divide el primer término del resto entre el primer término del divisor,
obteniéndose de este modo el segundo término del cociente.
❤ El
segundo término del cociente se multiplica por todo el divisor y el
producto así obtenido se resta del dividendo, cambiándole todos los
signos.
❤ Se
divide el primer término del segundo resto entre el primer término del
divisor y se repiten las operaciones anteriores hasta obtener cero como
resto.
TEOREMA DEL RESTO:

GRADO DE UN POLINOMIO
El grado de un polinomio de varias variables es el grado mayor de los términos del polinomio.
 Grado 3.
Grado 3.VALOR NUMÉRICO DE UN POLINOMIO
El valor numérico de un polinomio, P(x), para un valor x = a, es el número obtenido al sustituir la letra x por el número a y efectuar las operaciones indicadas. A ese número se le llama P(a).
Si P(a) = 0, se dice que a es una raíz o cero del polinomio P(x). Una raíz es una solución de la ecuación P(x) = 0.

INECUACIONES
Es una DESIGUALDAD entre dos expresiones algebraicas de una o varias incógnitas, que solo se verifica para ciertos valores de esas incógnitas; se expresa con los signos >, <, ≥ y ≤.
"< " Menor que "≤." Menor o igual que
Se puede representar en dos distintas formas:
1º La recta real
2º En intervalo/s
PRIMER GRADO:
PARÁBOLAS
Para esta parábola he utilizado GEOGEBRA
Primero, he descargado una foto de Benito Pérez Galdós.
Después he hecho 3 variables, punto "f", "g" y "h".
y otra de mi paseo por Roma (coliseo romano)
Para conseguir estas parábolas he tenido que poner (X - Y)^2
Para que la parábola tenga su punto más alto, he tenido que poner después de (X-Y)^2 - Z
Para que la parábola tenga su punto más bajo, he tenido que poner después de (X´-Y)^2 +Z
PARÁBOLAS INVERSAS
Parte de la función madre X:1
BICUADRADAS
IMPORTANTE
Una BICUADRADA es una ecuación de cuarto grado donde falta los términos X^3 y X
Pongamos un ejemplo:
x^4 -10x^2+9=0
Y hay una pequeña regla:
Vamos a decir que X^2 es igual a "t"
Y eso significa que X^4 es igual a "t^2"
y convertiremos nuestra ecuación y nos quedará:
t^2 -10t +9=0
Y ahora solo utilizaremos la regla para resolver cualquier ecuación de segundo grado (explicado en el otro tema de POLINOMIOS)
Se obtiene por la división que está al lado. Como no se sabe si tenemos que sumar o restar, una solución será 10+8 dividido entre 2 (9)Si nos fijamos en la solución de la fórmula, vemos que "t" tiene dos posibles soluciones: 9 y 1
O restando 10-8 dividido entre 2 (1)
El último paso es pasar las soluciones de "t" a "x" ( Las soluciones de abajo)
En X^2, tenemos dos soluciones, 3 y -3
Y en X^4 tenemos 1 y -1.
PONGAMOS OTRO EJEMPLO: (Un poco más difícil)
TENGAMOS SIEMPRE EN CUENTA QUE X^2= T EN LAS BICUADRADAS
9x^4 +2x^3 + 3x^2 + 2 = 8x^4 + 2x^3
Como veis, está el término X^3 y arriba he dicho que tiene que ser una bicuadrada cuando no tenga los términos X^3 Y X.
Bien, para saber si se trata de una bicuadrada y no es una confusión, pasaremos 8x^4 + 2x^3 hacia el otro lado para que esta ecuación sea igual a 0.
Mejor dicho, agruparemos todos los términos hacia la izquierda y para hacer eso, calculamos:
+9x^4 +2x^3 +2
-8x^4 -2x^3
1x^4 0x^3 +2
Como podemos ver ya no hay término X^3 y mucho menos X, a si que ahora sí es una bicuadrada
El siguiente paso es aplicar la regla de que X^2 = T:
Y nos quedaría: t^2 +3t +2 = 0
Después, resolveremos la ecuación de segundo grado con la fórmula:
Las soluciones son t= -1 y t=-2
Es decir, x debe cumplir: x^2= -1 o x^2=-2
Como -1 es negativo, ningún valor de x^2 podrá cumplir x^2 = -1
Como -2 es negativo, ningún valor de x^2 podrá cumplir x^2 = -2
Esto significa que esta ecuación no tiene SOLUCIÓN REAL.
IDENTIDADES NOTABLES
Si son ecuaciones donde intervienen las identidades notables deberíamos saber las 3 fórmulas:
La primera fórmula: Una identidad positiva, aparece cuando un binomio está entre paréntesis, al cuadrado y con un signo "+" en el medio.
También, si nos situamos en el otro lado del "=" significa que para obtener (a + b)^2, "a" tiene que estar multiplicada por sí misma (elevada a 2 o al cuadrado) + "a" multiplicada por 2 y después por "b" + "b" multiplicado por sí mismo (elevado a 2 o al cuadrado)
Ejemplo:
(a + b)^2 = a^2 + 2ab+b^2
(x + 5)^2 = x^2 + 2 x5 + 5^2 = x^2 + 10x +25
La segunda fórmula: Una identidad negativa, aparece cuando una binomio está entre paréntesis, al cuadrado y con un signo "-" en el medio.
Si no situamos en el desarrollo del binomio (al otro lado del "=") significa que "a" debe de estar multiplicado por sí mismo - "a" por 2 y por "b" + "b" multiplicado por sí mismo
Ejemplo:
(a - b)^2 = a^2 - 2ab + b^2
(x-4)^2= x^2 - 2x4 + 4^2 = x^2 - 8x + 16
La tercera fórmula: Una "suma por diferencia" aparece cuando hay dos binomios (uno en positivo y otro en negativo) multiplicados.
Para resolver este problema, lo único que hay que hacer es restar "a" al cuadrado con "b" al cuadrado.
Ejemplo:
( a + b) (a - b) = a^2 - ^2
(x + 7) (x-7) = x^2 + 7^2 = x^2 - 49
ECUACIONES DE 2º GRADO
Para que sea una ecuación de segundo grado, debe de llevar una "x" elevada al cuadrado
Fórmula : ax^2 + bx + c
Se llaman "coeficientes" a los términos "a" "b" y "c"
¿Cómo lo resuelvo?
Con esta simple fórmula:
EJEMPLOS
Como en la fórmula anterior hay dos signos juntos, ( el + y el -) siempre hay una doble solución, X 1 cuando el problema final se hace sumando y X 2 cuando el problema final se hace restando
¡¡¡¡¡RECUERDA!!!!!
Una raíz cuadrada con un número negativo no se puede resolver, significa que la ecuación no tiene solución real.
FACTORIZAR DE 1 NÚMERO
Significa que a un número lo llegas a expresar en factores primos: (Me explico)
Aquí, se ve como claramente el número 120 lo expresamos en números primos (2,3 y 5)
120= 2^3· 3· 5
¿CÓMO DIVIDIR POLINOMIOS?
Para dividir hay varios métodos:
1ºRuffini:
Es la división de un polinomio por un polinomio.
Primero se ordena el dividendo y el divisor con respecto a una misma letra.
Después, se divide el primer término del dividendo entre el primer término del divisor, obteniéndose así el primer término del cociente.
Se multiplica el primer término del cociente por todo el divisor y el producto así obtenido se resta del dividendo, para lo cual se le cambia de signo y se escribe cada término de su semejante. En el caso de que algún término de este producto no tenga ningún término semejante en el dividendo, es escribe dicho término en el lugar que le corresponda de acuerdo con la ordenación del dividendo y del divisor.
Se divide el primer término del resto entre el primer término del divisor, obteniéndose de este modo el segundo término del cociente.
El segundo término del cociente se multiplica por todo el divisor y el producto así obtenido se resta del dividendo, cambiándole todos los signos.
Se divide el primer término del segundo resto entre el primer término del divisor y se repiten las operaciones anteriores hasta obtener cero como resto.
2º Teorema del resto
El resto de dividir P(x) entre (x - a) es igual a P(a), valor númerico del polinomio en x = a.
RETO DE LA BOTELLA
¿Qué hacer para que mi botella caiga de pie?
Para todo problema, necesitamos varios pasos para solucionarlo:
1º EXPLORACIÓN: Simplemente tenemos que conocer el problema (¿De qué va?)
2º DISEÑO: Cuando ya conozcamos el problema, aportaremos ideas posibles entre todos,( ¿Qué se puede importar?)
3ºDESARROLLO Y ¡ EN MARCHA!: Lo siguiente que haremos es poner en marcha las ideas anteriores (¿Cuál será un éxito?)
4º ANÁLISIS Y NUESTRA REFLEXIÓN: ¡ Es hora de apuntar! Apuntaremos los resultados del apartado anterior, tanto fallos como aciertos.
5º DIFUSIÓN: Como el mismo paso dice, difundiremos nuestro trabajo hecho hasta ahora y al publicarlo, pueden decirnos si hay algún error o si está incompleto o si les gustó.
6º EVALUACIÓN DEL PROBLEMA: Para finalizar, haremos una pequeña conclusión y nos daremos cuenta si lo hemos hecho bien o mal.
Volviendo al tema de las botellas, hablaremos de las variables:
TENGAMOS EN CUENTA LAS PERSONAS EXPERTAS E INEXPERTAS ( diferentes resultados)
- CANTIDAD DE LÍQUIDO EN LA BOTELLA: Hemos probado con 1/2, 1/3 y 1/4
Nuestro grupo tuvo más éxitos con 1/4 que con otras medidas.
Para calibrar las botellas, llenamos las botellas a ojo, y después, para saber las medidas exactas, cogimos la pesa y no, ¡ No somos buenos en las aproximaciones!
-DISTANCIA DEL TIRADOR A LA MESA (o cualquier base): La mayoría e los tiros se han hecho sentados y a 1 metro de distancia de la mesa.
Aunque después intentamos cerca de la mesa y de pie y nos resultó más fácil que la botella cayer a de pie.
- BASE DE LA BOTELLA: En esta variable, hemos comprobado que la botella con la mejor base es la botella de "FUENTE UMBRIA".
TENGAN EN CUENTA QUE DE TANTO TIRAR LA BOTELLA SE VA ABOYANDO LA BASE DE LA BOTELLA Y NO TENDRÁ TANTAS POSIBILIDADES DE QUE CAIGA DE PIE.
- IMPULSO DE LA BOTELLA: Justamente este apartado lo comprobé yo y en mi opinión y mi experiencia, hay más probabilidades de que caiga de pie si se tira con una fuerza medida ya que si la tiras demasiado lento, la botella no llegará a la base y si se tira demasiado fuerte, rodará por la base pero no caerá de pie o no tocará la mesa.
-PERSEVERANCIA: Este es el apartado más importante, nuestro grupo tiró unas 30 veces cada uno, la perseverancia en este trabajo es el número de veces que tiras la botella.
- ÁNGULO EN EL QUE TIRAS LA BOTELLA:Me explico, con esto quiero decir, la posición de la muñeca al tirar la botella, nuestro grupo ha intentado que no varíe demasiado.
Aunque después intentamos cerca de la mesa y de pie y nos resultó más fácil que la botella cayer a de pie.
- BASE DE LA BOTELLA: En esta variable, hemos comprobado que la botella con la mejor base es la botella de "FUENTE UMBRIA".
TENGAN EN CUENTA QUE DE TANTO TIRAR LA BOTELLA SE VA ABOYANDO LA BASE DE LA BOTELLA Y NO TENDRÁ TANTAS POSIBILIDADES DE QUE CAIGA DE PIE.
- IMPULSO DE LA BOTELLA: Justamente este apartado lo comprobé yo y en mi opinión y mi experiencia, hay más probabilidades de que caiga de pie si se tira con una fuerza medida ya que si la tiras demasiado lento, la botella no llegará a la base y si se tira demasiado fuerte, rodará por la base pero no caerá de pie o no tocará la mesa.
-PERSEVERANCIA: Este es el apartado más importante, nuestro grupo tiró unas 30 veces cada uno, la perseverancia en este trabajo es el número de veces que tiras la botella.
- ÁNGULO EN EL QUE TIRAS LA BOTELLA:Me explico, con esto quiero decir, la posición de la muñeca al tirar la botella, nuestro grupo ha intentado que no varíe demasiado.
Este proyecto empezó el 14 de Diciembre.
A continuación, pondré un resultado en porcentajes de los inexpertos:
El porcentaje exacto de 1/2 es 7%
El de 1/3 es 41%
Y el de los Expertos:
1/2 con un porcentaje de 20%
1/3 es de 62%
1/4 con 83%
EN CONCLUSIÓN (respecto a las gráficas):
-Tanto a expertos (David Alba y Brayan Yanascual) como a inexpertos (Laura Balsa, Lisbeth Cordero y Nelson Andrés Castañeda) se nos da mejor las medida 1/4, mejora los aciertos si es con la botella fuente umbría y de pie cerca de la base.
-Como podemos apreciar, un medio tiene más fallos que aciertos en las dos gráficas, aconsejo no intentar más este reto con un medio.
-Y, por último, ha quedado una pequeña diferencia entre los inexpertos y expertos ya que los expertos superan la mitad de los aciertos y los inexpertos no.
Hay que decir que los expertos y los inexpertos se eligieron a raíz de las personas que practicaban este reto o que lo haya intentado más de 3 veces.
yo fui una inexperta ya que nunca había tirado la botella.
El lugar donde se realizó el proyecto fue en el aula detrás de Cali.
MI CONCLUSIÓN
( Sobre el proyecto)
Me ha parecido muy interesante este trabajo, deberíamos hacer más proyectos así porque lo más importante es aprender pero... ¡Si te puedes divertir mejor!
Sobre las conclusiones del trabajo en sí pienso que tirar 30 veces la botella me parece poco, deberíamos haber tenido más tiros.
Había un apartado en las variables que decía, "vueltas que da la botella" yo no he puesto ese apartado ya que no estoy de acuerdo, la mayoría de los tiros no llegan a dar una vuelta.
No he podido subir los videos ya que intenté subir uno y mi blog se bloqueó y se me borró todo lo escrito y no me voy a arriesgar.
¡Muchas Gracias por mirar mi blog!
NÚMEROS REALES
PASAR DE FRACCIÓN A DECIMAL
Para obtener la expresión decimal de una fracción, se hace la división del numerador entre el denominador.
8/4= 2 ⇒ Natural 4
9/4= 2,25 ⇒ Decimal exacto 4
8/4= 2 ⇒ Natural 4
9/4= 2,25 ⇒ Decimal exacto 4
4/3= 1,333333.... = 1,3 ⇒ Decimal periódico puro 7)
7/6= 1,166666.... = 1,16 ⇒ Decimal periódico mixto
Decimales exactos:
N = 2,38
100N = 238
N = 2, 38/100
Decimales periódicos puros:
N = 2,38
100N = 238
N = 2, 38/100
Decimales periódicos puros:
N= 2, 38 __
100N= 238,38
99N=236
N= 236/99
NÚMEROS IRRACIONALES
Números racionales son los que se pueden poner como cociente de dos números enteros. Su expresión decimal es exacta o periódica.
Números irracionales son los no racionales, es decir, los que no pueden obtenerse como cociente de dos números enteros. Su expresión decimal es infinita no periódica.
Hay infinitos números irracionales, algunos de los cuales son especialmente interesantes:
- La diagonal del cuadrado de lado 1: 2
- Si p no es cuadrado perfecto, p es irracional.
- En general, si p es un número entero y n p no es un número entero (es decir, p no es una potencia n-ésima), entonces n p es irracional.
- La diagonal de un pentágono de lado unidad: 2 15 + =φ (“fi”: Número áureo)
- En general, si p es un número entero y n p no es un número entero (es decir, p no es una potencia n-ésima), entonces n p es irracional.
- La diagonal de un pentágono de lado unidad: 2 15 + =φ (“fi”: Número áureo)
- La relación entre la longitud de una circunferencia y su radio: Π (“pi”)
Si en una recta situamos un origen (el cero, 0) y marcamos la longitud unidad, a cada punto le corresponde un número racional o un número irracional. Es decir, a cada punto de la recta le corresponde un número real. Por eso, a la recta numérica la llamamos recta real.
TRIGONOMETRÍA
Grado sexagesimal:
Si se divide la circunferencia en 360 partes iguales, el ángulo central correspondiente a cada una de sus partes es un ángulo de un grado (1°) sexagesimal.
Un grado tiene 60 minutos (') y un minuto tiene 60 segundos ('').
¿QUÉ ES LA RADIÁN?Es la medida de un ángulo cuyo arco mide un arco.
¿ QUÉ ES EL SENO?
Es la razón entre el cateto opuesto al ángulo y la hipotenusa
¿QUÉ ES EL COSENO?
Es la razón entre el cateto contiguo al ángulo y la hipotenusa.
¿QUÉ ES LA TANGENTE?
Es la razón entre el cateto opuesto al ángulo y el cateto contiguo al ángulo.
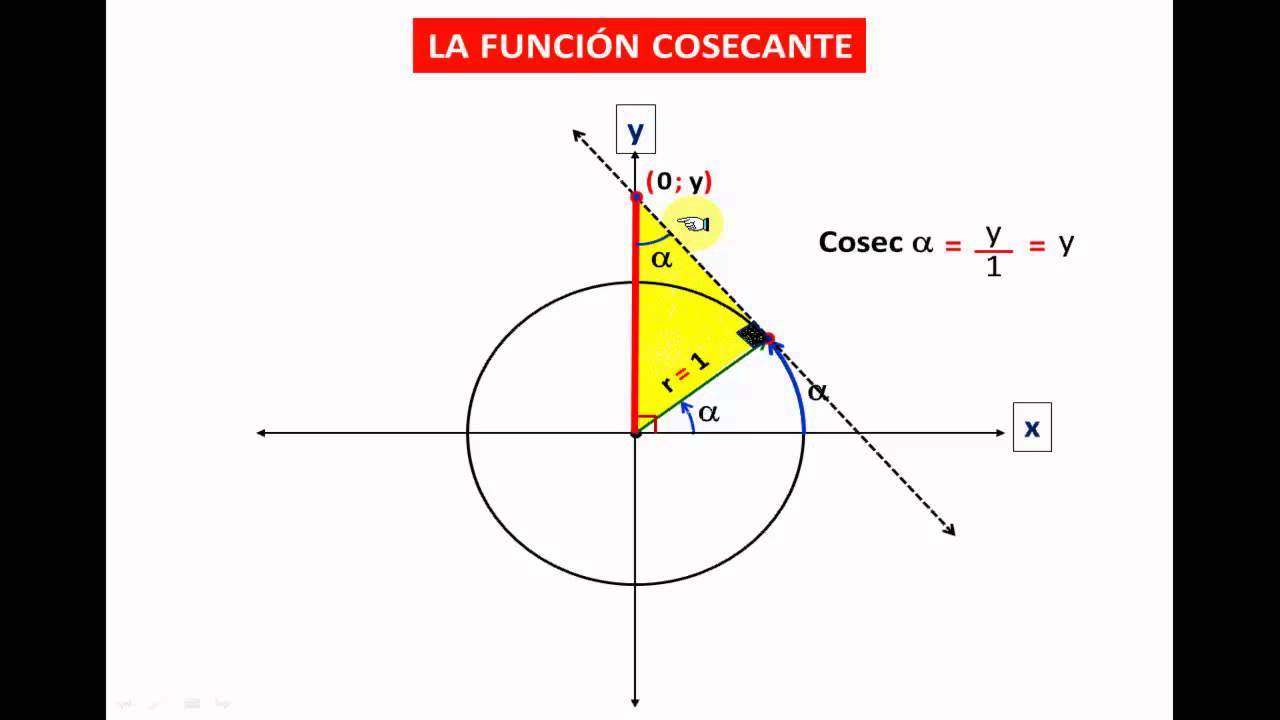
¿QUÉ ES EL COSECANTE?
Es la razón inversa del seno.
¿QUE ES LA SECANTE?
Es la razón inversa del coseno
¿ QUÉ ES LA CONTANGENTE?
Es la razón inversa de la tangente.
REDUCCIÓN AL PRIMER CUADRANTE
Un ángulo puede estar situado en cualquiera de los cuatro cuadrantes de la circunferencia. Los valores de sus correspondientes razones trigonométricas dependen de su posición.
ÁNGULOS SUPLEMENTARIOS
Ángulos suplementarios son los que suman 180º. Si el valor de un ángulo es "A", el valor del suplementario será "180º-A".
La relación de las razones trigonométricas de un ángulo con las de su suplementario va a permitir "reducir" ángulos del segundo al primer cuadrante.
ÁNGULOS COMPLEMENTARIOS

Ángulos complementarios son los que suman 90º. Si el valor de un ángulo es "A", el valor del suplementario será "90º-A".
La relación de las razones trigonométricas de un ángulo con las de su complementario va a permitir "reducir" ángulos del cuarto al primer cuadrante.NOTACIÓN CIENTÍFICA
Esta semana, a casa grupo nos ha tocado un tema, y el nuestro fue la notación científica donde yo y mi compañeros explicamos qué es, para qué sirve y cómo funciona.Nos hemos repartido el tema en partes, y yo ahora explicaré mi parte del tema y enqué medios he buscado:
DEFINICIÓN: La notación científica es un recurso matemático que sirve para simplificar cálculos y representar en forma breve números muy grandes o muy pequeños. Para hacerlo se usan las potencias de 10.
EL NÚMERO MULTIPLICADO POR LA POTENCIA DE 10 (N) SERÁ ENTRE 1 Y 10.
Su fórmula es: N X 10^x
Para expresar el número en notación científica:
- Primero: Se identifica la coma decimal (si la hay)
- Segundo:La desplazamos hacia la izquierda (si el exponente de 10 es positivo) o
- Tercero: Se rueda la coma tantos lugares como el número de exponente tenga 10 (x)
EJEMPLO:
7,341 X 10^6 = 0,000007341 ( Se a rotado la coma 6 veces)
2,3654 X 10^-4 = 23654 ( Se ha rotado la coma 4 veces)
Primero tenemos que saber las dos notaciones:
N1 X 10^x1 y N2 X 10^x2
Después, saber cómo multiplicarlas:
N1 X N2 X 10^x1 + x2 (Se suma los dos exponentes de 10 de cada operación)
EJEMPLO:
5,24 X 10^6 Y 6,3 X 10^8
(5,24 X 10^6) X (6,3 X 10 ^8) = 5,24 X 6,3 X 10^6+8 = 33,012 X 10^14 = 3,3012^15
¿CÓMO DIVIDIR CON LA NOTACIÓN CIENTÍFICA?
Primero tenemos que saber las dos notaciones:
N1 X 10^x1 y N2 X 10^x2
Después, saber cómo dividirlas:
(N1: N2) X 10^x1 - x2 ( Se resta los dos exponentes de 10 de cada operación)
EJEMPLO:
5,24 X 10^7 Y 6,3 X 10^4
(5,24 : 6,3)X 10^7-4 = 0,831746 • 10^3= 8,31746 • 10^-1 • 10^3 = 8,31746 • 10^2
Aquí un vídeo que les puede servir de mucho: https://www.youtube.com/watch?v=ok-IRe6ACaI
¿QUÉ HE APRENDIDO ESTA SEMANA?
En primer lugar, quería decir que con el cuadernillo de porcentajes que nuestra profesora nos ha dado, me ha venido bien para recordar hacer el tanto por ciento, como calcular aumentos y disminuciones porcentuales, calcular porcentajes mentalmente...etc.
Aparte, también aprendí unos pequeños trucos para calcular el problemas de porcentajes con algunos trucos que las profesora nos dio y, por último pero no menos importante, recordé los números reales ya que admito que se me estaban olvidando los números irracionales

















 .
.

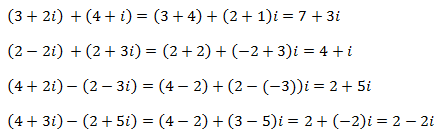











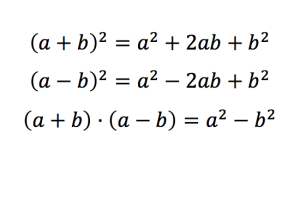












No hay comentarios:
Publicar un comentario